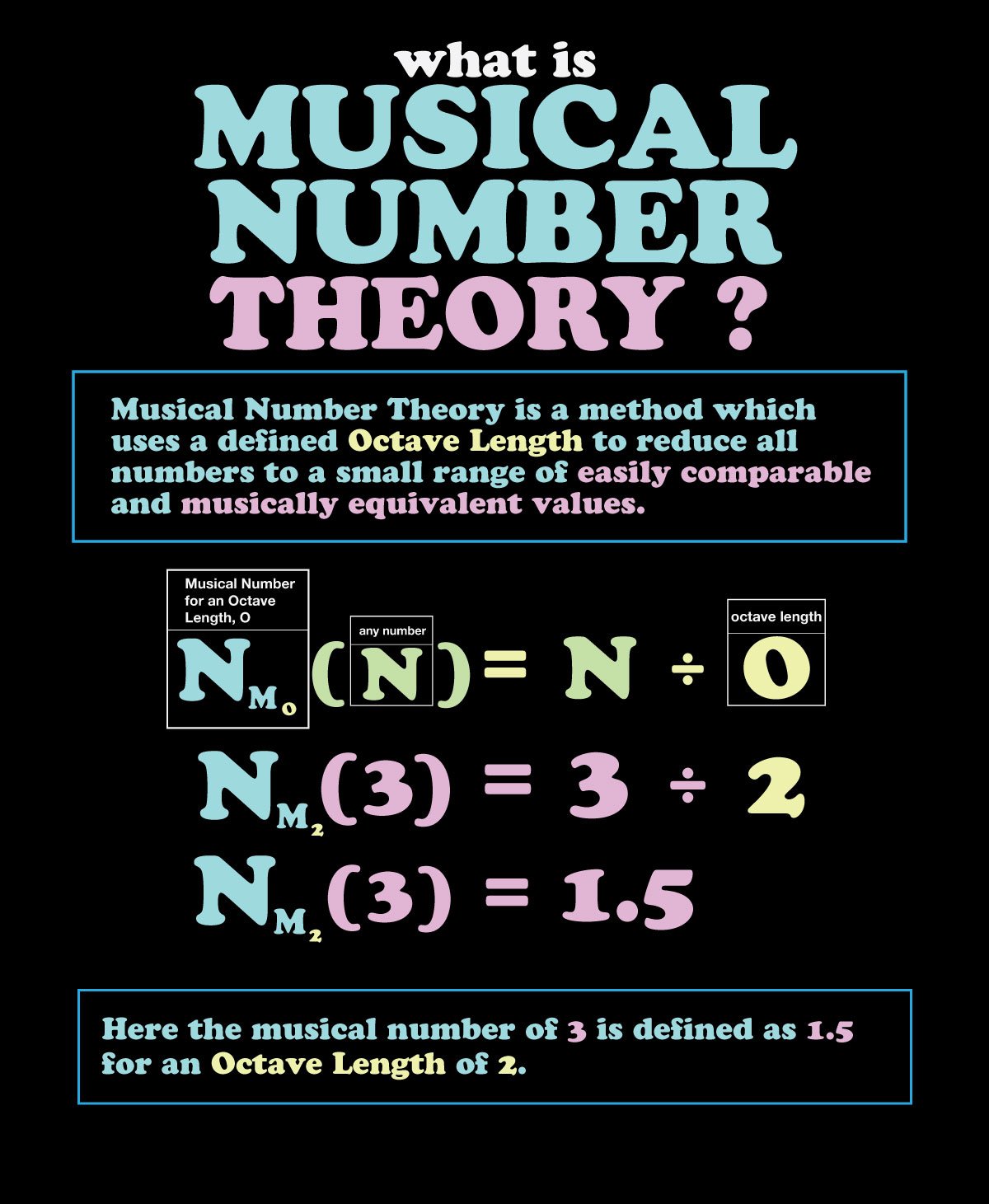A Three Part Journey

by Tale, by Number, by Science

Introduction

This piece is a 3 part foray into Harmony.

In the first part we explore some of the myth of Harmony, as in some ways it is a properly inspiring prelude to a strange object like Harmony’s Mirror. It is not necessary to read the myth before going into the math. But since this is a basic mathematical demonstration of what an harmonic mirror is, the second part gives the basic structure of calculating Harmonic Mirrors for any number or ratio. The math may be a bit daunting to some but it settles the primary objective of elucidating the structure of an harmonic mirror and how it’s made.

In part 3, I show some early experiments in musical number theory where the physical constants of nature are explored for their harmonic properties.

1

A Mytholoogical Prelude to Harmony’s Mirror

For those who would hear a tale of legend become reality, I offer here a sort of mythical account of the nature of Harmony. Not only as a cautionary tale of love and conquest, but as a clear example of how myth can inform us of the broader spectrum of the effects of art on our world.

The Mirror described here has mostly to do with the old Greek tale of Harmonia’s Necklace.

In this tale, Harmonia is the illegitimate daughter of Ares, the God of War, and Aphrodite, the Goddess of Love.

Hephaestus, the God of Craft, finds that his wife Aphrodite has had an affair with the God of War (one of her many affairs, if the tales are to be believed). So Hephaestus creates a wedding gift for her in the form of a necklace which will curse the progeny of all who wear it. Harmony’s Necklace was said to be most beautiful and of a finer craft than any mortal could muster. And yet it’s value lay in its power to preserve the beauty and youth of its wearer. All who possessed and wore the necklace knew great triumph and great tragedy. Though the necklace was said to hold all of Harmony’s power within it—a peaceful and preservative power—the bearer of the cursed necklace might know little of peace and quiet in this life. And so the necklace went through many bearers, from the mother of Dionysus, to the mother and wife of Oedipus, until finally it ended up in the Temple of Athena at Delphi where it might harm no mortal again.

So Harmonia was married to Cadmus, and the necklace was given to her as a gift of a beauty equal to its bearer. They knew great triumphs of conquest in their marriage—establishing an empire of nations. But before they ever could enjoy the fruits of empire, they both met their ends in human form to become transformed into serpents. And so, very much like the serpent which lingered at the Tree of Knowledge, the jewel of Harmony’s necklace was said to be held by an Amphisbaena, a serpent with 2 heads, something like the image below.

“The golden Necklace has been described thoroughly, but, briefly stated, it represented an amphisbaina, which is a two headed serpent, with open mouths as if hissing. The two mouths on each side enclosed with their jaws a golden eagle upright, its wings covered with yellow jasper and moonstone…” (Nonnus, Dionysiaca 5. 135 ff)

The jewel of Harmonia’s Necklace was said to hold the magical power of Harmony herself. I would submit that as you will see in this article (see the slides which define harmony above or below for a short form of this idea), Harmony is created by the convergence of 2 “heads” which are regarded as one and the same, as the octave length as it is here defined always starts at 1 and ends at another number (in western music we use 2). Very much like the fabled marriage of Harmony and the King, the nature of Harmony is also defined by a particular conception of Union.

The presence of the Eagle described above has an aspect of military and cultural dominance, as well as a touch of the old higher wisdom to it. The eagle soars high—an animal whose nature brings it closer to the Sun and to a higher plane of perspective than the earthbound animals. Eagles and birds of all sorts have long been thought of as messengers from the Divine. The divine message in this case is Harmony itself: held securely by a serpent with 2 heads, the jewel of Harmony’s Necklace is somehow all these years later the perfect mythical foil of a mathematical artifact: Harmony’s Mirror is an idealized form of a very real thing—a jewel of infinite facets which contains the power of Harmony within it.

You can consider this an attempt, much like in a pulp adventure tale, to show how myths can be very real—and how the artifacts of myth do indeed lead to all sorts of drama.

Luckily though, in this case none could possess Harmony’s Mirror (or the jewel of Harmonia’s Necklace) any more than they already do. As far as I can tell, all lifeforms are harmonic mirrors, just as all things are. Every atom we are made of is define by cycles, cyclical vibration, oscillation, and discreet energetic states of excitation and rest. Though it is mainly for Mathematicians, Scientists and enthusiasts, part 2 will provide the groundwork for a conception of Harmony beyond borders—even as much it defines those self-same harmonic limitations. Part 3 is for now quite short but it also includes an experiment in Musical Cosmos Theory, using harmonic mirrors to analyze the constants in nature.

So let us look into the jewel of Harmony’s Necklace in the only way that I currently know how.

2

A Mathematical Mirror

Prelude to the Mathematical Description

of Harmonic Mirrors

This is a portrait of time as much as any jewel. But the sequence of mirrors erected at the top of the page is the only way I know how to make the portrait.

This construction is made for one purpose, to see how time and frequency interrelate through harmonic reflections in a mirror which never stops reflecting. In fact, the only way this mirror seems to stop reflecting musical intervals is when the interval is a perfect musical number in a system we can easily calculate.

The strategy is to find the harmonic systems which resonate with any interval. And so not only time but also distance takes form in harmony’s mirror—which makes of every measure an infinite chain of musical harmonies.

This Imaginary Mirror reveals a quality of the Musical Form of Nature no matter how large, how small or how distant. The only reflections this mirror makes are chiral—which contradicts the very idea of a mirror in some ways. So in some ways this is also a very basic description of chiral number theory, where the reflection of one temporal cycle length is its inverse. Maybe the only comparable physical mirror would be a seriously warped one, where a really large object would always reflect as a very small object, and vice versa.

But in order to see this still-life portrait of time, you must make of the whole universe into a peculiar sort of temporal thread. To make the thread you must transform time into frequency and take one innocent leap of faith. A Period Length divided by its corresponding frequency is equal to 1.

This is only true because that is the definition of frequency- cycles per second, or Hertz ( Herz in German means Heart). In some sense this is measuring the Universe to the Human heart rate, which beats at a frequency of 1 to 2 Hz for an average adult. In another sense, if this mirror is used to compare two different things it acquires a more lively shared pulse (which then isn't necessarily a comparison to the human heart rate).

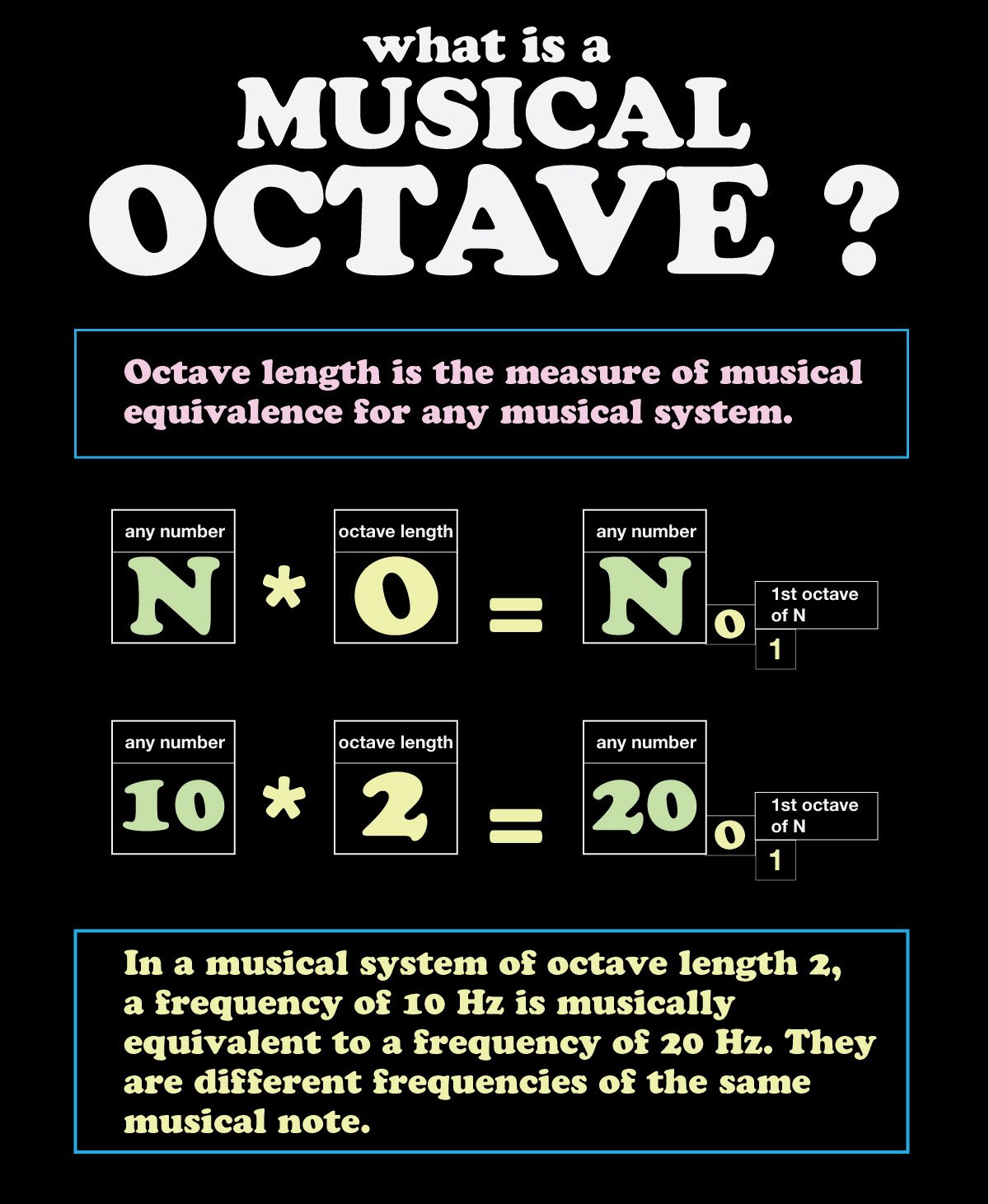
What you will see in Harmony’s Mirror is that any thing that vibrates or repeats makes music. But in order to see it the whole Universe must be reduced to 1. Or at the very least it must be reduced to what in music is known as One Octave length (see the image sequence above).

No matter how far or how close it is, all things are here measured between 1 and 2, if the octave length is 2.

One is the Universal Note in all musical form. But if all you have is one, then it really is a simple sort of music, where each is regarded as 1—and in some ways it precludes a shared sense of time. 2 is the next to simplest musical measure of time, and it governs the system of western harmony used in music to tune and design instruments. So even though 2 seems pretty simple there is all the complexity of the Universe within its bounds, especially if you define everything between one and two.

Harmony’s Mirror can reflect all different forms of music whether it is using 2, 3 or any other octave measure, or whether you use a 5, 12 or 1200 note musical system.

Time comes in 2 forms simultaneously here, once as a cycle that repeats (or a length of time), and once as an equivalent frequency of vibration.

They make a chiral pair that reflect each other perfectly in any octave length, even though they will have different reflections and pairs in different harmonic mirrors, especially if those mirrors use different octave lengths.

Suffice it to say you are in for some sort of a strange ride. In order to see a portrait of time, we will briefly sketch out some of the mathematical territory and then we will measure out an Harmonic Mirror.

Measures of a Mirror

There is a version of Harmony’s Mirror for every scale of measurement, especially scales of time and when vibration is a factor.

But the question of what unit of measure to use is somewhat less important than using the same one for everything you hold up to any particular harmonic mirror.

It should be noted that what follows is applicable to any repeated thing, though the power of Harmony’s Mirror is much greater with consistent repetition.

A cycle is assumed to be anything that repeats
The temporal length, T, of any cycle has a corresponding frequency, 1/T.
Resonance, R, is defined as a ratio proportion between any 2 quantities measured in the same scale and property.
or
T1/T2= R
The ratio or resonance of a cycle of any length in time, T, to its frequency, 1/T is
T/(1/T) = T^2 (Equation 1)
T^2 also has a corresponding frequency defined by 1/T^2 in the same fashion as in the second statement above.
This strategy can then be repeated for every successive power of the original cycle length, T, as every successive power of T or 1/T is simply the octave equivalent of T or 1/T and so is harmonically the same note within its own octave length.

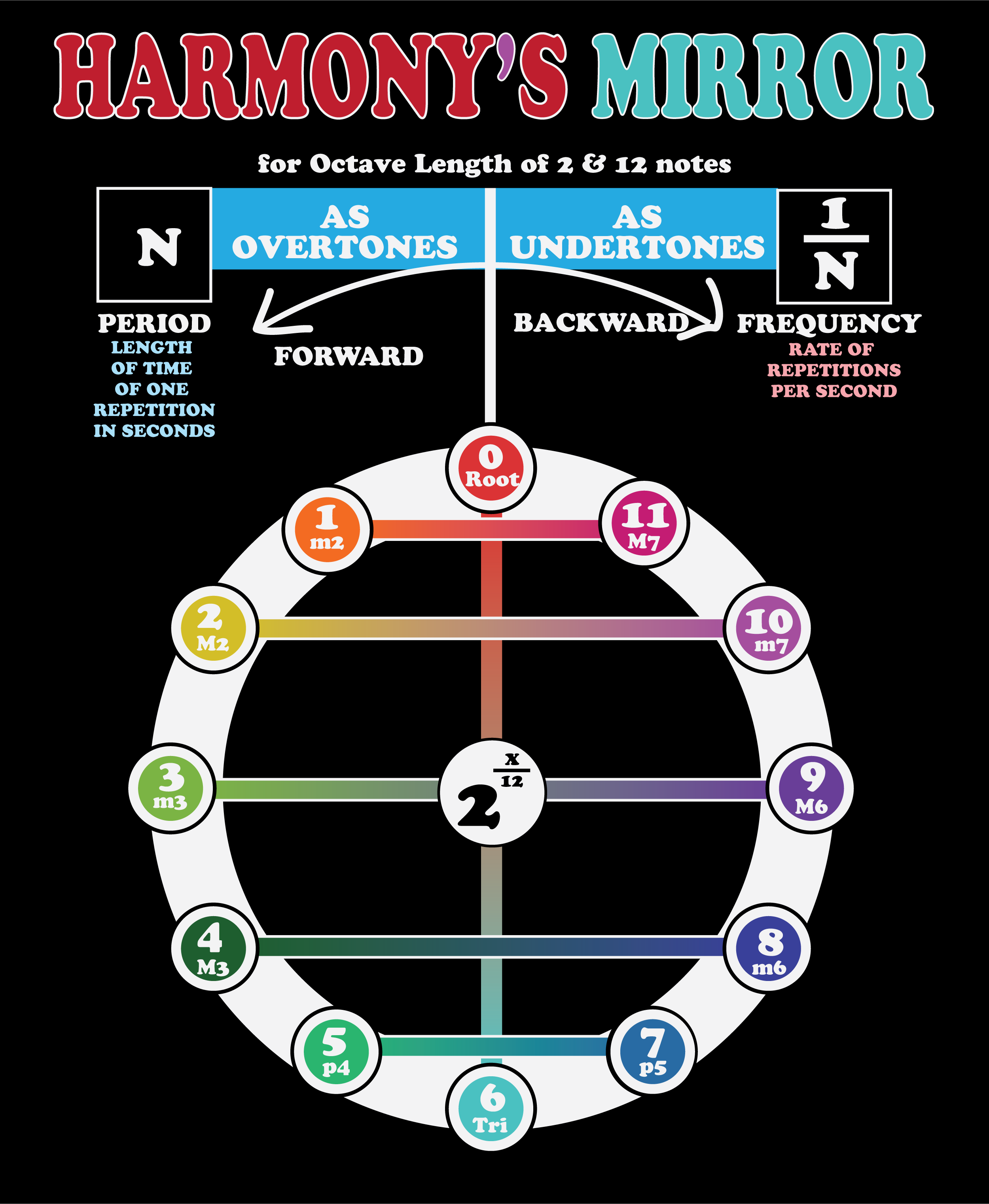
Musical Number Theory

In order to construct an harmonic mirror, it is essential to brush up on a few more musical math concepts which help to make this whole picture a lot clearer. Below is a sequence of images which defines some of these ideas in a slideshow form. Before now, I am not sure if anyone ever heard of the term musical number theory. So the basic math here uses the concept of the musical or harmonic octave to reduce all real numbers to harmonic numbers (intervals), so that they may be harmonically analyzed.

Harmony’s Mirror is a mathematical method of translating any resonance ratio into a musical interval and finding what harmonic systems that interval exists in for any octave length as it is regarded as an endlessly reflecting mirror of time and frequency. I used this specifically for planetary cycles that are long recurring—like day lengths and year lengths. So it is a way to help identify the nearest native musical systems of any planetary or systemic resonance for any octave length.

Harmony’s Mirror was constructed to find the shared native harmonic systems of any resonance relationship. The closer a musical number gets to a perfect interval in a harmonic system it becomes trapped within via the methodology. So in some sense it is a finer measure of resonance than you could ever need for any application.

For Harmony’s mirror the measurements are in logarithmic or exponential scales, which are here based on the number 2. So a perfect scale of 12 equal parts is defined by equal exponential slices (as seen above). For an octave length of 2, 12 equal slices is defined by 2^(1/12), 2^(2/12), 2^(3/12)….. etc…

Using perfect musical numbers as a start I was able to determine some of the basic structures of Harmony’s Mirror.

A musical number, 2^(1/12)=1.0596 has its inverse 1/2^(1/12) or 2^(11/12).

Here we have what is called a minor second and a major seventh in music.

In Harmony’s Mirror they are perfect chiral reflections or a chiral pair for this octave length. In a world of relative proportions, the one always implies the other because the only question is which one you start from and which way down or up the musical spiral you are going in comparison to your staring point.

The second chiral pair is defined by the ratio of the original pair to one another (regarded as a ratio in its own right), or

2^(1/12)^2 = 2^(2/12).

This then yields a major second, which is also the musical distance in one direction that the original chiral pair has from one another on a musical mirror.

The second chiral pair is defined by the inverse of 2^(2/12), or 2^(10/12).

One of the simplest ways to do this math, which focuses even more on the music, uses a very simple equation.

For an octave length of 2, Musical numbers (see slides above) always satisfy the relationship Nm1*Nm2=2 amongst chiral pairs. This is a simple extension of n ÷ n = 1, except since the musical measure of equivalence here is the octave length of 2, we multiply both sides of the equation by 2. The reduction of all numbers (or at least one of the 2 in question) to their equivalent musical numbers must take place before equation 2 below can be of use.

2^(1/12) * 2^(11/12) = 2

or

Nm1 * Nm2 = 2 (Equation 2)

or alternatively and more beautifully I think

Nm(n) * Nm(1/n) = 2 (Equation 3)

What it means is that any musical number, Nm1, of a real number, n, has an inverse chiral musical twin Nm2, with regard to any octave length, O, defined by

O/(Nm(n)) = Nm(1/n)

For octave length of 2, we have

2/(Nm(n)) = Nm(1/n)

The third chiral pair of 2^1/12 is defined by the ratio of the second chiral pair to one another. But for clarity I will do the first 3 pairs, which will hopefully show the pattern more clearly.

Nm(n) * Nm(1/n) = O(x) (Eq. 1.1)
(1st chiral pair and the primary Reflection for any octave length, x)
Nm(n) / Nm(1/n) = Nm(n^2) (Eq. 1.2)
(Secondary reflection)
Nm(n^2) * Nm(1/n^2) = O(x) (Eq. 2.1)
(Second Chiral Pair)
Nm(n^2) / Nm(1/n^2) = Nm(n^4) (Eq. 2.2)
(Tertiary reflection)
Nm(n^4) * Nm(1/n^4) = O(x) (Eq. 3.1)
(Third Chiral Pair)

This scheme continues ad infinitum or until the pattern becomes an endless loop. But it also depends on what your starting number is.

In this case we started with the number 2^(1/12).

Running it through an Harmonic Mirror….

Nm(2^(1/12))= 2^(1/12)

1.1 2/ 2^(1/12) = 2^(11/12) (first chiral twin)

1.2 (2^(1/12))^2 = 2^(2/12) (secondary reflection)

2.1 2/2^(2/12) = 2^(10/12) (chiral twin of the second reflection)

2.2 (2^(2/12) )^2 = 2^(4/12) (tertiary reflection)

3.1 2 / 2^(4/12) = 2^(8/12) (chiral twin of the tertiary reflection)

3.2 (2^(4/12) )^2 = 2^(8/12) (quaternary reflection)

4.1 2 / 2^(8/12) = 2^(4/12) (chiral twin of the quaternary reflection)

In this scheme you can see how the loop begins at the “third level of reflection,” or in tertiary reflection. The pattern goes back and forth in a loop between 2^(4/12) and 2^(8/12) by the third reflection in this Harmonic Mirror.

This example has helped to illustrate a particular pattern of harmonics with a mirror constructed of 12 equal parts to an octave length of 2. But it is worth stating that other mirrors have very different properties in terms of their reflective patterns.

This is an illustration of a very basic mirror in a very basic case. Hopefully it shall provide some basic tools to calculate and construct Harmonic Mirrors for mathematical testing and exploration.

Concepts in a HARMONIC SYSTEMS THEORY and Musical Cosmos Theory

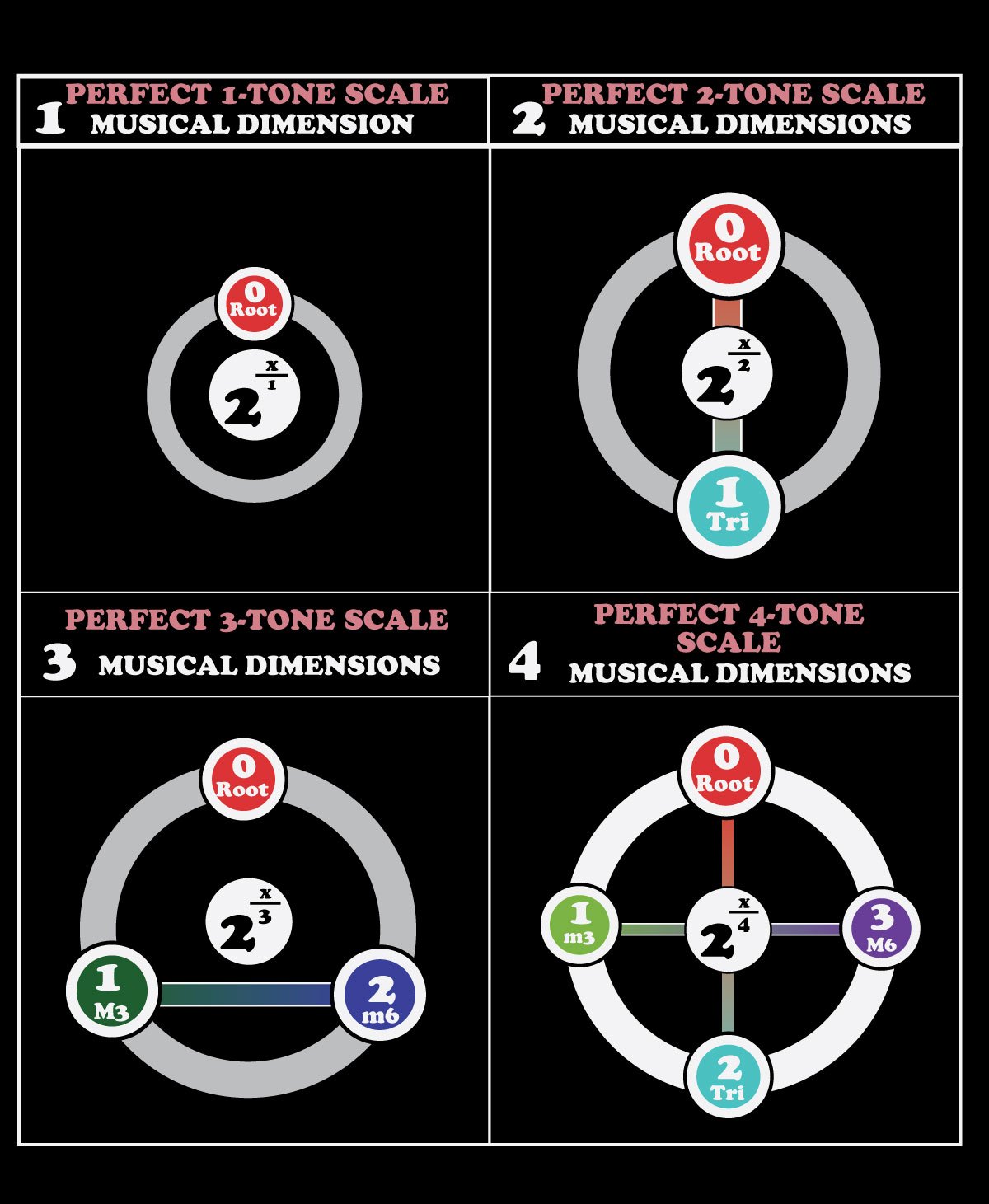
Musical Dimensionality

One of the more interesting qualities of music from the perspective of musical cosmos theory is dimensionality.

For western music we use a system of 12 musical points or notes. Above, we constructed what I would call an Harmonic Mirror of octave length 2, and 12 points.

It is also worth stating that each Mirror is also a construction of its own musical dimension.

In some ways what is implied is that some things resonate within particular musical dimensions in a specific way which is entirely invisible or in a different form in another musical dimension.

If the mirror illustrated above were to reflect time which resonates within another dimension the reflections would be variously Harmonic or not quite so Harmonic at all, depending on the Musical Dimension through which you are scrying.

Chiral Number Theory

What is most interesting in musical math is also that it seems to imply chirality in music and resonance as one of its basic and defining properties. If you go the same distance from one point in two different directions, you arrive at two different musical measures of distance.

Travel a perfect fifth (3/2 or 1.5) forward from the root note and you arrive at a perfect fifth.

Or 1 * 1.5 = 1.5

Travel backwards a perfect fifth and you arrive at a perfect fourth.

Or 1/1.5 = 2/3

And since 2/3 * 2 = 4/3 you have a perfect fourth.

What it means is that chirality is the consequence of a logarithmic conception of time or measure. And since every cycle contains not only a particular pattern of resonance within a set of musical dimensions, each particular musical dimension defines chirality in its own way.

3

Prelude to the Physics of Harmony’s Mirror

One of the main uses i have put to this mathematical construction I call Harmony’s Mirror concerns the harmonics of basic constants and measures of the physical world. In some ways the basic use of an harmonic mirror is to take any measure or ratio between like measures and plug it into the Mirror.

Harmony’s Mirror works quite literally with distances, lengths of time, and frequencies. Mass is analogous to amplitude or weight here, which is to say that mass adds power or potency to any resonance ratio or note. The effect is to drown out everything else the more mass an Harmonic system has within any musical dimension or any particular configuration of an harmonic mirror.

In the case of a particular physical constant of nature, which recurs in a great number or all cases of a certain type, there you have a number which can be studied in more detail as to its dimensional preferences and the strengths of its particular harmonic form within different musical systems.

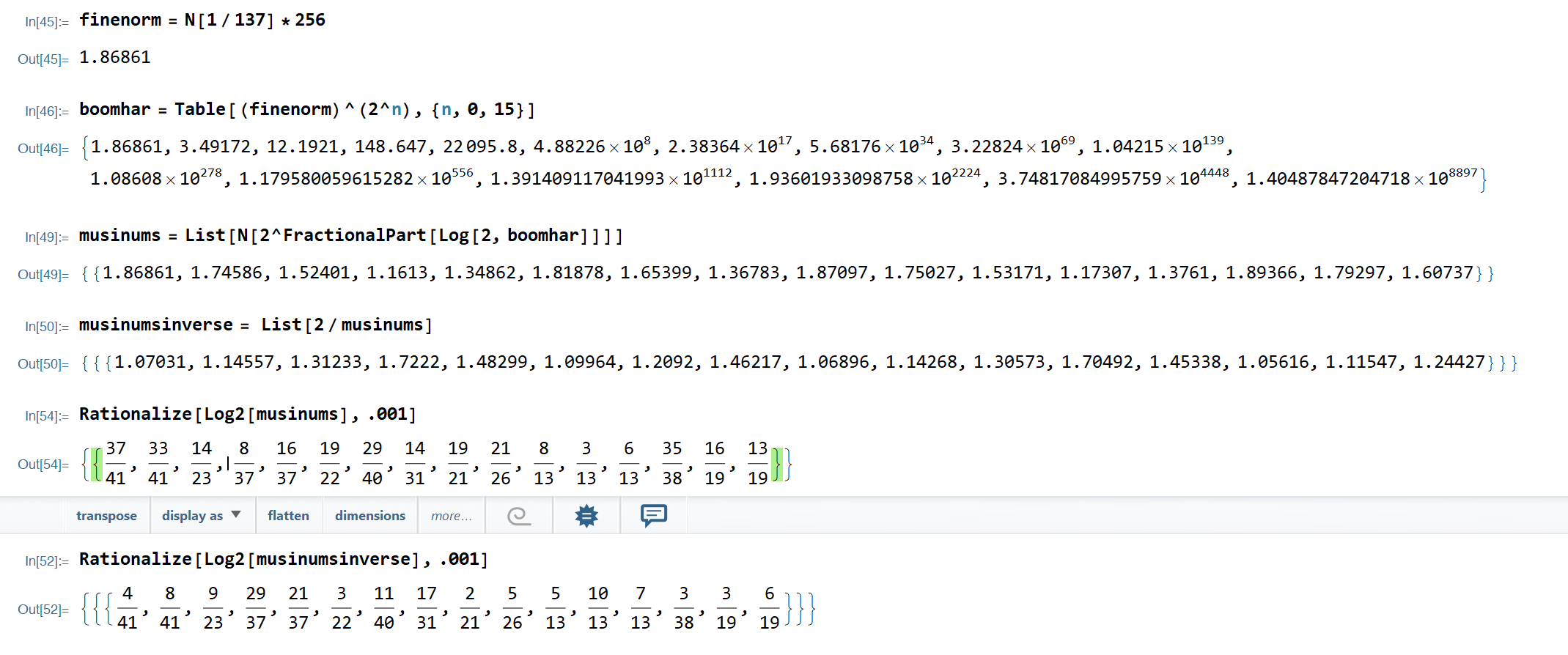
For the fine structure constant, the resonance seems to be within a 13 or 26 point octave of 2, because 26 includes a 13 part octave perfectly, though a 41 part octave of length 2 is the immediate dimension of resonance.

( All of the examples illustrated here have been normalized for musical math by multiplying or dividing by 2 until it is a number between 1 & 2. The reason this has been done is because I am unable to calculate some of the mirrors otherwise even on my very powerful pc because some of the numbers are so large or small. The results are the same, it just means less work for the computer. )

Figure 2. Here is measure of the musical properties of the fine structure constant as seen through an harmonic mirror. Here 13 (which is also included in 26) musical dimensions or parts is favored as well as 19, 37, and 41. This is denoted by the bottom 2 rows of fractions above. Here the top part of the fraction is the particular note in question, and the bottom part of the fraction is the number of parts or dimensions the musical octave is split into.

Figure 3. Here is measure of the musical properties of the gravitational constant as seen through an harmonic mirror. Here 31 musical dimensions or points is favored as well as 16. This is denoted by the bottom 2 rows of fractions above. Both 31 and 21 are shared between the fine structure constant and the gravitational constant.

Figure 4. Here is measure of the musical properties of the planck constant as seen through an harmonic mirror. Here an octave of 23 musical dimensions is favored. This is denoted by the bottom 2 rows of fractions above. Also 21 is favored here in the planck constant , which makes it the musical dimension of choice for planck, fine structure, and gravity with systems of an octave length of 2.

Of course, you may be wondering, “what is the meaning of all this musical information about the physical constants?” To a degree it simply means that physical systems resonate within these musical dimensions more than in others. But even then certain musical dimensions are very resonant with others by their nature. For instance, a 26 point octave of length 2 includes a 13 point octave of length 2 perfectly. It is also perhaps just as important that nearby dimensions often have near “overlap” points where they are quite close musically (within 1%, as seen below in Figure 5).

Scrying Harmony’s Mirror