A Derivation of Harmonic Axioms of Energy from Wave Mechanics, Music and simple Arithmetic

updated on 3.22.22

What follows is a technical essay which is written to lay a general foundation for a Musical Cosmos Theory based on cyclic patterns and wave mechanics, which is not based on the vagaries of human perception. The math that is involved is mostly simple arithmetic. We will be using a series of charts on Music Theory, Wave Mechanics, and what i have been calling the NASA Planetary Data Sheet, which is freely available on the web and is also partially a compiled data sheet that I have made over the last few years.

Below is a logarithmic music spiral overlaid on a linear scaled circle.

The strategies employed for making sense of the planetary data sheet are in part derived from what I call musical number theory, which is a way of basing your understanding of ratio on “musical ratios” and of reducing all numbers to an expression of a power of 2. It is the same region of mathematics as Harmonic Numbers though instead of using e (2.71…) or the natural logarithmic function, I use 2 and the log base-2, which is more helpful as a way to calculate harmonic ratios between things in alignment with the musical octave and its associated wave mechanics.

Making Waves Together

If all energy and matter is understood as vibration and resonance or even as stuff that vibrates and resonates, then we are always firmly within the territory of wave mechanics which answers the question of how energy works. All atoms vibrate, and so all matter of that type vibrates and is therefore a territory of wave mechanics (vibration in air is what makes sound waves, acceleration of an electron makes a photon--which is a type of vibration or oscillation in the electromagnetic field).

We will take the simplest situation of 2 waves that come into contact and superpose upon one another their respective energies and vibrations. The simplest way i know to illustrate these ideas is to use the simplest case: one note or frequency of vibration, superposed with itself in a higher register or octave. The octave is a special case of vibration where the doubling of a cyclic or recurring pattern to twice the speed (or cutting the speed in half) has very distinct properties of cancellation and amplification with its original rate of vibration. In rhythm too there are special properties in the doubling or halving of the tempo that don’t hold at other nearby tempos. (see note 1)

Even with this one note example we can see some very interesting properties of Harmony and Resonance which will help also to establish a fuller idea of musical and energetic Harmony from the simplest case as a foundation for the celestial and energetic ideas employed here.

Figure 1: A definition of the 12 Tone Harmonic Series

Figure 2: Basic Demonstration of Combined Frequencies

From Figure 2 above we have a basic idea of what the simple arithmetic of combining a wave with itself will look like. A wave at 2 Hz combined with another 2 Hz wave will potentially create certain extremes of additive and subtractive effects depending on their phases and a number of other properties. This is the simplest case where we are considering 1 dimension which is two waves from 2 different sources converging and combining. You could also imagine it as two martial artists punching at 2 punches per second at one another, but it is more like two punches on the same face at the same time. From opposite directions the head might get crushed in on itself or break both of the hands coming in. From the same direction the head might be sent across the room along with its body at twice the force and the unfortunate victim may indeed hear a high pitched sound in his head for a while afterwards too.

The scenario of punchers only goes so far perhaps.

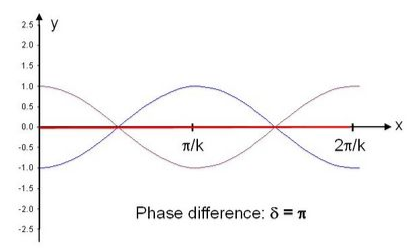
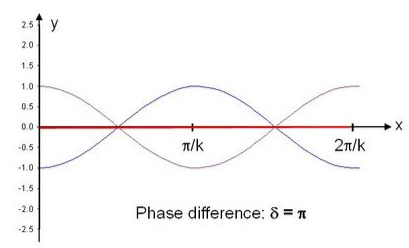
**Figure 3**- phase opposition
Phase opposition or two notes sung at the same pitch will cancel out each other when sung at a particular timing equal to one half the wavelength of both tones, which results in the red line above or the difference frequency of Zero because the waves cancel each other out (red line).

Two waves of the same frequency can cancel each other or make a Void or Null.

Or 2 waves of the same frequency can amplify each other and also imply an octave by summing the 2. This also means that by the rhythm or timing there is implication of the higher tonality of the same note. So as the musicality gets higher by rhythm and where 2 notes are the same, we have octave harmonies implied--which would also seem like a basic way in which certain types of repetition solidify octave notes and types of harmony in the imagination and in fields of energy (and because wave mechanics is the province of energy fields).

In the case of nullification they also imply a double cycle or an Octave span. So in this sense two vibrations of the same frequency, or in Prime Unison as it is called, can combine or subtract in specific ways to cancel each other or imply a higher register octave harmony of the original notes.

The idea of combining frequencies in such a fashion is used as a simple way of understanding Harmony and Resonance rather than an exhaustive proof of method. Though recently i have learned of ways in which the simplest form of a wave equation includes summation and differences frequencies as a very real aspect of any wave, most of what I take from this chart above is more of a theoretical gauge for energetic tendencies in any situation.

On top of that it is good to state here at the outset that what we have in the middle column labelled MUSIC is a set of frequencies that exist at lower levels of amplification that are not necessarily heard by the listener but which are implied by the simple arithmetic of adding or subtracting in the case two notes that are the same or at octave intervals apart in frequency. Just as implied harmony or near harmony is often heard without being played when you tune a many stringed intrument, so too do certain rhythms have their flavor by not playing the implied rhythm in the way it is predictably heard by the listener.

A Word on Timing

When you play two notes of the same frequency together in music, the timing of those notes is every bit as important as the frequency. For example, if you play all the notes of a melody in a different tempo and phrasing, then the melody is unfortunately not the same melody--it is a different melody composed of the same notes.

In wave mechanics just as in music the timing is a key factor of Harmony and Resonance.

A Word on Degrees of a Circle and the Musical Spiral

Some schools of thought differ as to their breaking the degrees of a circle according to a logarithmic style or a linear one. If we are to be perfectly harmonious in our mapping to allow for multiple dimensions of a thing to become clear, we should venture to match the rules and manner of the numbers and their forms that we are working with. So by the more linear regarding of the degrees of a circle we would have 1 lap around a circle equals 1. The second lap equals 2. So you might reach the opinion like I did that 1.5 laps is therefore 180 degrees, or if 1 and 2 are 360 as in the musical spiral above, 1.5 is assuredly on the other side as it is half the distance.

The only problem with that idea is that if you split up the distance between 1 and 2 into 12 different parts, then by its own logarithmic logic 2^(6/12) = 2^(1/2)= 1.414, not 1.5. So in some ways it is perhaps more preferable to use 1.414 = 180 degrees instead.

This would mean that the holy perfect fifth would be at 210 degrees. By astrological thinking, which may indeed seem irrelevant to some, 210 degrees is a very gentle or weak influence. Kepler and many others who have pondered and explored the Musica Universalis, or the music of the universe, in the scientific and mathematical work would have agreed that such massive spheres of influence could not fail to affect us and our humble world, especially as these spheres have shaped space and time around us for billions of years.

You might think, “what does it matter that 180 degrees is a perfect fifth or Tritone (called the Devil’s Note or the Blue Note in modern blues music)?” The difference only comes into play if there is some perceptible difference in those two intervals. If I play them slowly or never together you may notice less of a difference, than if played in sequence and in rhythm. But if you use a tritone in any chord in place of a perfect fifth you notice a difference immediately. The Tritone sounds harsh, strange and otherworldly, where the perfect fifth substituted in the same chord sounds powerful, supportive and full. Rock and pop music use the power chord and the octave more than any others. Very few songs you hear feature the Tritone in anything more than a passing glance in any performance or radio song. The reason is because it creates a harsh and oppositional tonal energy. With that sad, what you will see below is that with an octave span of 2, the perfect fifth is the first ratio implied by combined frequency math other than its own frequency or an octave relative.

Perhaps this says something about the character of the perfect fifth as one of the weakest resonances of the root. Incidentally I think this is what makes the perfect fifth so important. How not to overshadow the root note or erase its character? Energetically speaking, what we see in the following picture is perhaps more about cyclically supportive energy, not the destructive variety.

A Single Tone in 6 ways

Using the idea of Combined or Superposed frequencies and simple arithmetic we have a set of Harmonic ratios arrived at by only one note and its properties when combined or subtracted with itself at the same or higher registers. Here it is also good to state that since wave mechanics is primarily concerned with physical matter and energy this chart also has implications which are very real and as universal as waves and wave energy are.

Same tone - Void or Higher Union. For 2 notes that are the same, or in Prime Unison Harmony, we arrive at the ideas of Void, a higher Octave, Octave Unsion (higher union) and the span of an octave.
2 tones an octave apart - Supportive opposition and the common or original Root. For 2 notes an octave apart we arrive at the idea of a higher perfect Fifth (or cyclic or opposition by the linear account or 210 degrees by log) and by subtraction also we arrive at the original Root frequency, which in music is called Prime Unison and it is also the case of two notes exactly the same as in the first example.
By the second Octave or a factor of 4 apart the 2 frequencies imply both a higher major Third (or what is the same in Astrology as a Square by linear, 120 degrees by log or in wave mechanics and time is a quarter cycle) and a perfect Fifth which is between the two frequencies that are 2 octaves apart.
By the third Octave or a factor of 8 apart the 2 frequencies imply both a higher major Second or whole Tone(or what is the same in Astrology as a semi-Square (or by log 60 degrees or sextile) or in wave mechanics and time is an eighth of a cycle) and a major Seventh (for the root frequency) or a minor Second or half Tone down (for the higher frequency)--both of which are between the two frequencies that are 3 octaves apart.
By the fourth Octave or a factor of 16 apart the 2 frequencies imply both a higher minor Second or half Tone by addition; and a major Seventh (for the root frequency) or a minor Second or half Tone down (for the higher frequency) by subtraction which is between the two frequencies that are 4 octaves apart.
By the fifth Octave or a factor of 32 apart we start to see how the harmonies (quarter Tones) involved are becoming more and more dissonant and less perceptibly different than the original frequencies.

With Figure 2 we have the basic harmonic and temporal (time-based) ideas which are fairly universal to music, whether it is tonal or not. And yet they are simply ratios that have resonance using only one tone (and therefore all tones) as a starting point.

It is also worth stating that time in this example, as in all examples, is a strictly cyclic or circular thing on the physical level, not a straight line in any way except on the imaginary level (which is certainly not something which makes it irrelevant).

From the Figure 4 below we have an implication of an octave or higher vibration of the same tone and with the figure below we have the idea that prime Unison in phase unity amplifies the signal by 2 times. Combine two same frequency vibrations out of phase with one another by 180 degrees (or cyclically opposed) and you arrive at both an implied and real cancellation of energy (Figure 3 above or Figure 5 below). The difference is in the timing.

Figure 4 : *Phase Union of two notes sung at the same pitch and the same time will double the amplification of the original tones (red line).*

Figure 5: Phase opposition or two notes sung at the same pitch will cancel out each other when sung at a particular timing equal to one half the wavelength of both tones, which results in the red line above or the difference frequency of Zero because the waves cancel each other out (red line).

What all of these cases imply in terms of energy is that when you combine energy that is of the same or an octave frequency relative, most of the implied Harmonies are oppositional or friction based if you regard the perfect fifth as 180 degrees (opposition, square, semi-square) except in the case of the destructive or subtractively timed frequencies one octave apart. In terms of physics some of the implied harmonies are also oppositional and perpendicular. In the case of 90 degree phase difference the effect is a more modest amplification than phase unity.

If you take the logarithmic version of the musical spiral we have a picture where 0, 30, 60, 120, and 210 are the astrological angles of the first 5 octaves which become most prominent. These are all very supportive angles, except that 210 and 120 form a nice 90 square that may add some weight to the idea of the most pleasant harmony, the perfect fifth, is supported and supplemented by the most pleasant angle of astrology to create a sort of sunny power harmonic that many do enjoy to hear, the major chord, or the Root with a Major 3rd and a Perfect Fifth.

Appendix

Human & Animal Factors of Harmony

The Primary Cycle of an Animal is the heartbeat. And so in terms of Harmony the most primary factor is in the interplay with those natural rhythms in communication or activity or what could be called the using the appropriate synchrony and harmonics in communication.

For a child human the general heart rates go between 100-150 beats per minute (or between 1.67 - 2.5 Hertz or cycles per second). For the average human adult, the heart rate is generally between 60 and 120 cycles per minute. A very basic idea here is that since the child's heart runs at a faster tempo they resonate with a higher tempo than adult humans. Perhaps this is an easy way to understand the need for kids to have faster paced entertainment, communications and games than adults. It is easier to work with things “in step” or in synchronous motion with you, the force of friction is lessened.

An adult cat’s heart rate is between 140 and 220 beats per minute. A kitten’s heart rate is between 220 – 260 beats per minute. So here again a cat processes energy at a higher rate than humans on average. And an adult cat effectively has a doubled rate compared to an adult human. This has an implied result, when harmonically timed, of emphasizing the human rate when subtractive (opposed in phase) and emphasizing the shared higher oppositional harmonic (higher Fifth) when in phase.

In electromagnetism opposition can occur where energy is attempting to regulate by position and timing the potentially destructive energies that would result by closer proximity or conjunction, as in the case of a 2 electron atom. In astrological lore, the opposition is also a polarized energy where things that are at war generate the potent energies of self-transformation which can be difficult to manage and yet they are the cornerstone of developing a more potent stability and a higher level of energy to work with, just as in the case of a 2 electron atom which requires a the addition of 3 particles in its nucleus to regulate the energy of the orbiting electrons.

I would wager that music (and cultural exchange) between humans and other animals would run most successfully along the lines of their respective heart rates than any particular melody or phrasing, though I would also wager that across species the simple chart of perfect Fifth, major Third, and major second and minor Second would be fairly universal as "harmonies" by rhythm or tone.

Celestial Patterns

Orbital Distance

Figure 5 - Planetary Orbital Distances

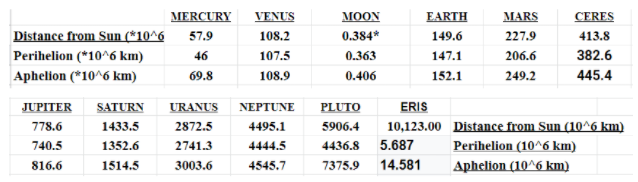
One of the simplest patterns of the planets in our solar system concerns distance. The octave structure of successively doubled distances holds well to the measured distances of the planets though it is certainly not perfect. However the octave structure of the solar system is certainly much more visible when you consider that though the mean distances from the sun aren’t perfectly aligned by the octave, the planets do nonetheless have a structure which overlaps via an octave structure which is more organic in nature. Consider the numbers below as a juxtaposition of perfect octave with the available planetary distances from the Sun.

50–100–200–400–800–1600–3200–6400–12800

If you correlate the above numbers to the chart you can immediately see the overlap. It isn’t quite perfect as a first attempt as Venus, the Earth, Saturn, Uranus and Neptune stand outside the perfect octave, yet they are quite close in even the most clumsy attempt to put them all in an octave structure. If the octave structure is adapted to include a more organic structure then the whole list of 12 planets included above fits into a perfect “adaptive” octave where no one series of successively doubled numbers is preferred or included. For instance, somewhere in its orbit the distance of Jupiter from the Sun (750 million km) is a perfect octave resonance of another point in Saturn’s orbital distance from the Sun (1500 million km). Using this organic or adaptive octave structure all the planets listed above exist in the same key, and only 2 planets, Earth and Neptune, are even a different note. This means that the solar system resonates most plainly as a mostly one note musical piece in terms of distance, and only a perfect fifth is the other note present (expressed by both Earth and Neptune).

In some sense the octave structure here embodied in the planets offers a sort of rough but ready proof of the musicality of matter and energy whether at the smaller scales or the largest.

In terms of planetary properties, the truly resonant and musical nature of celestial order is more visible from the perspective of the planetary Day lengths.

Solar Day Lengths

Figure 6: Planetary Spin Resonance within 2% of the 12 Tone Harmonic series

In the chart above, the blue indicates the presence of ratios that are harmonic in the same register as the others on the same horizontal plane. What it means specifically is that the entire solar system has resonance and harmonic interplay with others via their Solar Day lengths. On the top right of Figure 6, you can see how Venus, Mercury and our Moon are in nearly perfect alignment by the oppositional harmony of a perfect fifth, which is also the favored or most common planetary musical alignment by day length. The Sun and Pluto are in pretty close to Octave Unison from 2 octaves apart via their Day lengths (off by 2%). Other than that every planet or celestial body listed of the 12 in the main chart exist within a 2 percent standard of deviation from perfect musical alignment (besides Mars, which exists in an unlisted minor 2nd alignment with Eris)!

So whereas the Planets exist in a very organic form of Harmony by distance from the Sun, by the day length they are all in musical harmony with other planets in such a way that the whole system is in musical harmony—though not with all others. In some ways, the day length--which is unchanging--can be seen as the Harmonic which is accented, lessened or amplified by their relative distances to one another as they change over time.

Notes

1 - Double time can be played simultaneously with single time and continue to be rhythmically in synch, even though simultaneously playing at 60 bpm and 77bpm will be mostly out of synch in their entire conjunction. The analysis of octaves also applies perhaps to rhythm as it does to tonality. By octaves, the common factor is 2 and the harmonies are successively lower powers of two in the pattern of their sum frequencies. So it would seem that 60, 63.75, 67.5, 75, 90, 120 would all have some kind of continuous synchrony, depending perhaps upon the particular rhythm. Yet chaos theory would suggest that such harmonies as the perfect 5th are the critical point in tipping the scales of chaotic motion back to unison and repetition.

The Music of Energy